OpenACC Tutorial - Adding directives
| This site replaces the former Compute Canada documentation site, and is now being managed by the Digital Research Alliance of Canada. Ce site remplace l'ancien site de documentation de Calcul Canada et est maintenant géré par l'Alliance de recherche numérique du Canada. |
- Understand the process of offloading
- Understand what is an OpenACC directive
- Understand what is the difference between the loop and kernels directive
- Understand how to build a program with OpenACC
- Understand what aliasing is in C/C++
- Learn how to use compiler feedback and how fix false aliasing
Offloading to a GPU
The first thing to realize when trying to port a code to a GPU is that both the CPU located in the host and the GPU do not share the same memory:
- The host memory is generally larger, but slower than the GPU memory;
- A GPU does not have direct access to the host memory;
- To use a GPU, data must therefore be transferred from the main program to the GPU through the PCI bus, which has a much lower bandwidth than either memories.
This means that managing data transfers between the host and the GPU will be of paramount importance. Transferring the data and the code onto the device is called offloading.
OpenACC directives
OpenACC directives are much like OpenMP directives. They take the form of pragma statements in C/C++, and comments in Fortran. There are several advantages to using directives:
- First, since it involves very minor modifications to the code, changes can be done incrementally, one pragma at a time. This is especially useful for debugging purpose, since making a single change at a time allows one to quickly identify which change created a bug.
- Second, OpenACC support can be disabled at compile time. When OpenACC support is disabled, the pragma are considered comments, and ignored by the compiler. This means that a single source code can be used to compile both an accelerated version and a normal version.
- Third, since all of the offloading work is done by the compiler, the same code can be compiled for various accelerator types: GPUs or SIMD instructions on CPUs. It also means that a new generation of devices only requires one to update the compiler, not to change the code.
In the following example, we take a code comprised of two loops. The first one initializes two vectors, and the second performs a SAXPY, a basic vector addition operation.
| C/C++ | FORTRAN |
|---|---|
#pragma acc kernels
{
for (int i=0; i<N; i++)
{
x[i] = 1.0;
y[i] = 2.0;
}
for (int i=0; i<N; i++)
{
y[i] = a * x[i] + y[i];
}
}
|
!$acc kernels
do i=1,N
x(i) = 1.0
y(i) = 2.0
end do
y(:) = a*x(:) + y(:)
!$acc end kernels
|
Both in the C/C++ and the Fortran cases, the compiler will identify two kernels:
- In C/C++, the two kernels will correspond to the inside of each loops.
- In Fortran, the kernels will be the inside of the first loop, as well as the inside of the implicit loop that Fortran performs when it does an array operation.
Note that in C/C++, the OpenACC block is delimited using curly brackets, while in Fortran, the same comment needs to be repeated, with the end keyword added.
Loops vs Kernels
When the compiler reaches an OpenACC kernels directive, it will analyze the code in order to identify sections that can be parallelized. This often corresponds to the body of a loop that has independent iterations. When such a case is identified, the compiler will first wrap the body of the loop into a special function called a kernel. This internal code refactoring makes sure that each call to the kernel is independent from any other call. The kernel is then compiled to enable it to run on an accelerator. Since each call is independent, each one of the hundreds of cores of the accelerator can run the function for one specific index in parallel.
| LOOP | KERNEL |
|---|---|
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
|
void kernelName(A, B, C, i)
{
C[i] = A[i] + B[i];
}
|
| Calculates sequentially from index i=0 to i=N-1, inclusive. | Each compute core calculates for one value of i. |
The kernels directive
The kernels directive is what we call a descriptive directive.
It is used to tell the compiler that the programmer thinks this region can be made parallel.
At this point, the compiler is free to do whatever it wants with this information.
It can use whichever strategy it thinks is best to run the code, including running it sequentially.
Typically, it will:
- Analyze the code in order to identify any parallelism
- If found, identify which data must be transferred and when
- Create a kernel
- Offload the kernel to the GPU
One example of this directive is the following code:
#pragma acc kernels
{
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
}
The above example is very simple. However, code is often not that simple, and we then need to rely on compiler feedback in order to identify regions it failed to parallelize.
Those who have used OpenMP before will be familiar with the directive based nature of OpenACC. There is however one major difference between OpenMP and OpenACC directives:
- OpenMP directives are by design prescriptive in nature. This means that the compiler is required to perform the requested parallelization, no matter whether this is good from a performance stand point or not. This yields very reproducible results from one compiler to the next. This also means that parallelization will be performed the same way, whatever the hardware the code runs on. However, not every architecture performs best with code written the same way. Sometimes, it may be beneficial to switch the order of loops for example. If one were to parallelize a code with OpenMP and wanted it to perform optimally on multiple different architectures, they would have to write different sets of directives for different architectures.
- In contrast, many of OpenACC's directives are descriptive in nature. This means that the compiler is free to compile the code whichever way it thinks is best for the target architecture. This may even imply that the code is not parallelized at all. The same code, compiled to run on GPU or on CPU may therefore yield different binary code. This, of course, means that different compilers may yield different performance. It also means that new generations of compilers will do better than previous generations, especially with new hardware.
Example: porting a matrix-vector product
For this example, we use the code from the exercises repository.
More precisely, we will use a portion of the code from the cpp/matrix_functions.h file.
The equivalent Fortran code can be found in the subroutine matvec contained in the matrix.F90 file.
The C++ code is the following:
for(int i=0;i<num_rows;i++) {
double sum=0;
int row_start=row_offsets[i];
int row_end=row_offsets[i+1];
for(int j=row_start;j<row_end;j++) {
unsigned int Acol=cols[j];
double Acoef=Acoefs[j];
double xcoef=xcoefs[Acol];
sum+=Acoef*xcoef;
}
ycoefs[i]=sum;
}
The first change we make to this code in order to try to run it on the GPU is to add the kernels directive.
At this stage, we don't worry about data transfer, or about giving more information to the compiler.
#pragma acc kernels
{
for(int i=0;i<num_rows;i++) {
double sum=0;
int row_start=row_offsets[i];
int row_end=row_offsets[i+1];
for(int j=row_start;j<row_end;j++) {
unsigned int Acol=cols[j];
double Acoef=Acoefs[j];
double xcoef=xcoefs[Acol];
sum+=Acoef*xcoef;
}
ycoefs[i]=sum;
}
}
Building with OpenACC
The NVidia compilers use the -acc (target accelerator) option to enable compilation for an accelerator.
We use the sub-option -gpu=managed to tell the compiler that we want to use managed memory.
This managed memory simplifies the process of transferring data to and from the device.
We will remove this option in a later example.
We also use the option -fast, which is an optimization option.
[name@server ~]$ nvc++ -fast -Minfo=accel -acc -gpu=managed main.cpp -o challenge
...
matvec(const matrix &, const vector &, const vector &):
23, include "matrix_functions.h"
30, Generating implicit copyin(cols[:],row_offsets[:num_rows+1],Acoefs[:]) [if not already present]
Generating implicit copyout(ycoefs[:num_rows]) [if not already present]
Generating implicit copyin(xcoefs[:]) [if not already present]
31, Loop carried dependence of ycoefs-> prevents parallelization
Loop carried backward dependence of ycoefs-> prevents vectorization
Complex loop carried dependence of Acoefs->,xcoefs-> prevents parallelization
Generating NVIDIA GPU code
31, #pragma acc loop seq
35, #pragma acc loop vector(128) /* threadIdx.x */
Generating implicit reduction(+:sum)
35, Loop is parallelizable
As we can see in the compiler output, the compiler could not parallelize the outer loop on line 31. We will see in the following sections how to deal with those dependencies.
Fixing false loop dependencies
Sometimes, the compiler believes that loops cannot be parallelized despite being obvious to the programmer. One common case, in C and C++, is what is called pointer aliasing. Contrary to Fortran arrays, C and C++ do not formally have arrays. They have what is called pointers. Two pointers are said to be aliased if they point to the same memory. If the compiler does not know that pointers are not aliased, it must assume that they are. Going back to the previous example, it becomes obvious why the compiler could not parallelize the loop. If we assume that each pointer is the same, then there is an obvious dependence between loop iterations.
restrict keyword
One way to tell the compiler that pointers are not going to be aliased, is by using a special keyword. In C, the keyword restrict was introduced in C99 for this purpose. In C++, there is no standard way yet, but each compiler typically has its own keyword. Either __restrict or __restrict__ can be used depending on the compiler. For Portland Group and NVidia compilers, the keyword is __restrict. For an explanation as to why there is no standard way to do this in C++, you can read this paper. This concept is important not only for OpenACC, but for any C/C++ programming, since many more optimizations can be done by compilers when pointers are guaranteed not to be aliased. Note that the keyword goes after the pointer, since it refers to the pointer, and not to the type. In other words, you would declare float * __restrict A; rather than float __restrict * A;.
Declaring a pointer as restricted formally means that for "the lifetime of the pointer, only it or a value derived from it (such as ptr +1) will be used to access the object to which it points". This is a guarantee that the programmer gives to the compiler. If the programmer violates this guarantee, behaviour is undefined. For more information on this concept, see this Wikipedia article.
Loop directive with independent clause
Another way to tell the compiler that loops iterations are independent is to specify it explicitly by using a different directive: loop, with the clause independent. This is a prescriptive directive. Like any prescriptive directive, this tells the compiler what to do, and overrides any compiler analysis. The initial example above would become:
#pragma acc kernels
{
#pragma acc loop independent
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
}
Back to the example
Going back to the matrix-vector product above, the way that we recommend fixing false aliasing is by declaring the pointers as restricted. This is done by changing the following code in matrix_functions.h:
double *Acoefs=A.coefs;
double *xcoefs=x.coefs;
double *ycoefs=y.coefs;
by this code:
double *__restrict Acoefs=A.coefs;
double *__restrict xcoefs=x.coefs;
double *__restrict ycoefs=y.coefs;
We note that we do not need to declare the other pointers as restricted, since they are not reported as problematic by the compiler. With the above changes, recompiling gives the following compiler messages:
[name@server ~]$ nvc++ -fast -Minfo=accel -acc -gpu=managed main.cpp -o challenge
matvec(const matrix &, const vector &, const vector &):
23, include "matrix_functions.h"
27, Generating implicit copyout(ycoefs[:num_rows]) [if not already present]
Generating implicit copyin(xcoefs[:],row_offsets[:num_rows+1],Acoefs[:],cols[:]) [if not already present]
30, Loop is parallelizable
Generating Tesla code
30, #pragma acc loop gang /* blockIdx.x */
34, #pragma acc loop vector(128) /* threadIdx.x */
Generating implicit reduction(+:sum)
34, Loop is parallelizable
How is ported code performing ?
Since we have completed a first step to porting the code to GPU, we need to analyze how the code is performing, and whether it gives the correct results. Running the original version of the code yields the following (performed on one GPU node):
[name@server ~]$ ./cg.x
Rows: 8120601, nnz: 218535025
Iteration: 0, Tolerance: 4.0067e+08
Iteration: 10, Tolerance: 1.8772e+07
Iteration: 20, Tolerance: 6.4359e+05
Iteration: 30, Tolerance: 2.3202e+04
Iteration: 40, Tolerance: 8.3565e+02
Iteration: 50, Tolerance: 3.0039e+01
Iteration: 60, Tolerance: 1.0764e+00
Iteration: 70, Tolerance: 3.8360e-02
Iteration: 80, Tolerance: 1.3515e-03
Iteration: 90, Tolerance: 4.6209e-05
Total Iterations: 100 Total Time: 29.894881s
Running the OpenACC version yields the following:
[name@server ~]$ ./challenge
Rows: 8120601, nnz: 218535025
Iteration: 0, Tolerance: 4.0067e+08
Iteration: 10, Tolerance: 1.8772e+07
Iteration: 20, Tolerance: 6.4359e+05
Iteration: 30, Tolerance: 2.3202e+04
Iteration: 40, Tolerance: 8.3565e+02
Iteration: 50, Tolerance: 3.0039e+01
Iteration: 60, Tolerance: 1.0764e+00
Iteration: 70, Tolerance: 3.8360e-02
Iteration: 80, Tolerance: 1.3515e-03
Iteration: 90, Tolerance: 4.6209e-05
Total Iterations: 100 Total Time: 115.068931s
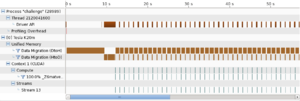
The results are correct. However, not only do we not get any speed up, but we rather get a slow down by a factor of almost 4! Let's profile the code again using NVidia's visual profiler (nvvp).
NVIDIA Visual Profiler
One graphical profiler available for OpenACC applications is the NVIDIA Visual Profiler (NVVP). It's a cross-platform analyzing tool for codes written with OpenACC and CUDA C/C++ instructions. Consequently, if the executable is not using the GPU, you will get no result from this profiler.
When X11 is forwarded to an X-Server, or when using a Linux desktop environment (also via JupyterHub with two (2) CPU cores, 5000M of memory and one (1) GPU), it is possible to launch the NVVP from a terminal:
[name@server ~]$ module load cuda/11.7 java/1.8
[name@server ~]$ nvvp
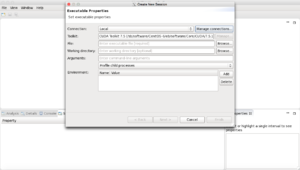
- After the NVVP startup window, you get prompted for a Workspace directory, which will be used for temporary files. Replace
homewithscratchin the suggested path. Then click OK. - Select File > New Session, or click on the corresponding button in the toolbar.
- Click on the Browse button at the right of the File path editor.
- Change directory if needed.
- Select an executable built from codes written with OpenACC and CUDA C/C++ instructions.
- Below the Arguments editor, select the profiling option Profile current process only.
- Click Next > to review additional profiling options.
- Click Finish to start profiling the executable.
This can be done with the following steps:
- Start nvvp with the command nvvp & (the & sign is to start it in the background)
- Go in File -> New Session
- In the "File:" field, search for the executable (named challenge in our example).
- Click "Next" until you can click "Finish".
This will run the program and generate a timeline of the execution. The resulting timeline is illustrated on the image on the right side. As we can see, almost all of the run time is being spent transferring data between the host and the device. This is very often the case when one ports a code from CPU to GPU. We will look at how to optimize this in the next part of the tutorial.
The parallel loop directive
With the kernels directive, we let the compiler do all of the analysis. This is the descriptive approach to porting a code. OpenACC supports a prescriptive approach through a different directive, called the parallel directive. This can be combined with the loop directive, to form the parallel loop directive. An example would be the following code:
#pragma acc parallel loop
for (int i=0; i<N; i++)
{
C[i] = A[i] + B[i];
}
Since parallel loop is a prescriptive directive, it forces the compiler to perform the loop in parallel. This means that the independent clause introduced above is implicit within a parallel region.
For reasons that we explain below, in order to use this directive in the matrix-vector product example, we need to introduce additional clauses used to manage the scope of data. The private and reduction clauses control how the data flows through a parallel region.
- With the private clause, a copy of the variable is made for each loop iteration, making the value of the variable independent from other iterations.
- With the reduction clause, the values of a variable in each iteration will be reduced to a single value. It supports addition (+), multiplication (*), maximum (max), minimum (min), among other operations.
These clauses were not required with the kernels directive, because the kernels directive handles this for you.
Going back to the matrix-vector multiplication example, the corresponding code with the parallel loop directive would look like this:
#pragma acc parallel loop
for(int i=0;i<num_rows;i++) {
double sum=0;
int row_start=row_offsets[i];
int row_end=row_offsets[i+1];
#pragma acc loop reduction(+:sum)
for(int j=row_start;j<row_end;j++) {
unsigned int Acol=cols[j];
double Acoef=Acoefs[j];
double xcoef=xcoefs[Acol];
sum+=Acoef*xcoef;
}
ycoefs[i]=sum;
}
Compiling this code yields the following compiler feedback:
[name@server ~]$ nvc++ -fast -Minfo=accel -acc -gpu=managed main.cpp -o challenge
matvec(const matrix &, const vector &, const vector &):
23, include "matrix_functions.h"
27, Accelerator kernel generated
Generating Tesla code
29, #pragma acc loop gang /* blockIdx.x */
34, #pragma acc loop vector(128) /* threadIdx.x */
Sum reduction generated for sum
27, Generating copyout(ycoefs[:num_rows])
Generating copyin(xcoefs[:],Acoefs[:],cols[:],row_offsets[:num_rows+1])
34, Loop is parallelizable
Parallel loop vs kernel
| PARALLEL LOOP | KERNEL |
|---|---|
|
|
Both approaches are equally valid and can perform equally well.
- Modify the functions matvec, waxpby and dot to use OpenACC. You may use either the kernels or the parallel loop directives. The directories step1.* from the Github repository contain solutions.
- Modify the Makefile to add -acc -gpu=managed and -Minfo=accel to your compiler flags.
<- Previous unit: Profiling | ^- Back to the lesson plan | Onward to the next unit: Data movement ->